
以前に 赤外線距離センサー において単振動を測定いたしました。 今回は前半ではこの運動を数値解析し、 後半で減衰のある振り子の運動を解析的に解きます。

単振動の実際のデータを解析します。もちろん、 振幅を減らしながら減衰していく運動となります。 以下が実測値と後半で示す理論式(41)を最小二乗法により あてはめた結果です。振動の端の方では パンダの左右へのブレがあるために誤差が大きくなっていますが、 減衰の様子、振動数が変化しないことなどが 数式でうまく表現できていることがわかります。
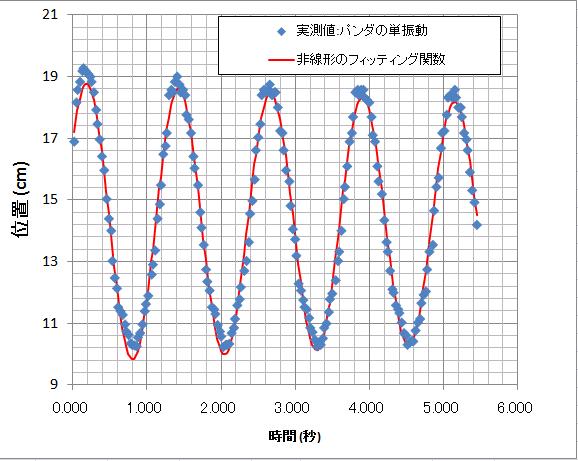
数式をy=C1*exp(-C5*t)*sin(2PI*C2*t + C3) + C4 として係数を求めました。 C1は振幅、C5は減衰、PIは円周率C2は周期、C3は初期の位置、 C4はセンサーから中心の位置に対応します。 最小二乗法には非線形になりますのでエクセルのソルバーを用いました。
紐の長さ(37 cm, 実測)から予想される周期は 1.22秒で、観察された周期(1.24秒,最小二乗法より)と かなり良い一致を示しています。パンダの模型の全体の 重さは101gでしたので、摩擦係数kはk=0.0056 m/sと 求められました。興味をもたれた方は、 このような条件で、以下の理論式のエクセルのシートが正しいかを 確認されると面白いと思います。
高校の物理か大学1年生くらいで習う振り子の単振動を解きます。 以下に、振り子の模式図を示します。

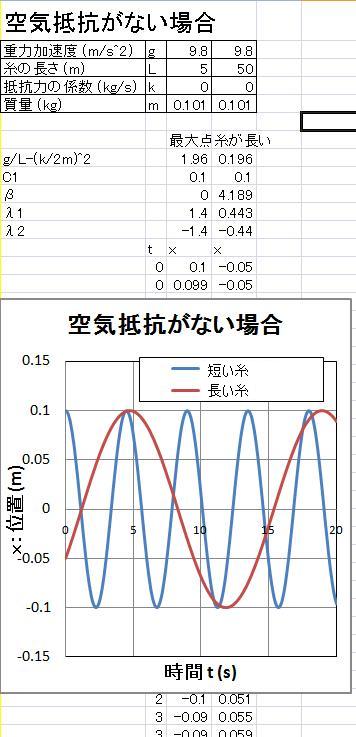
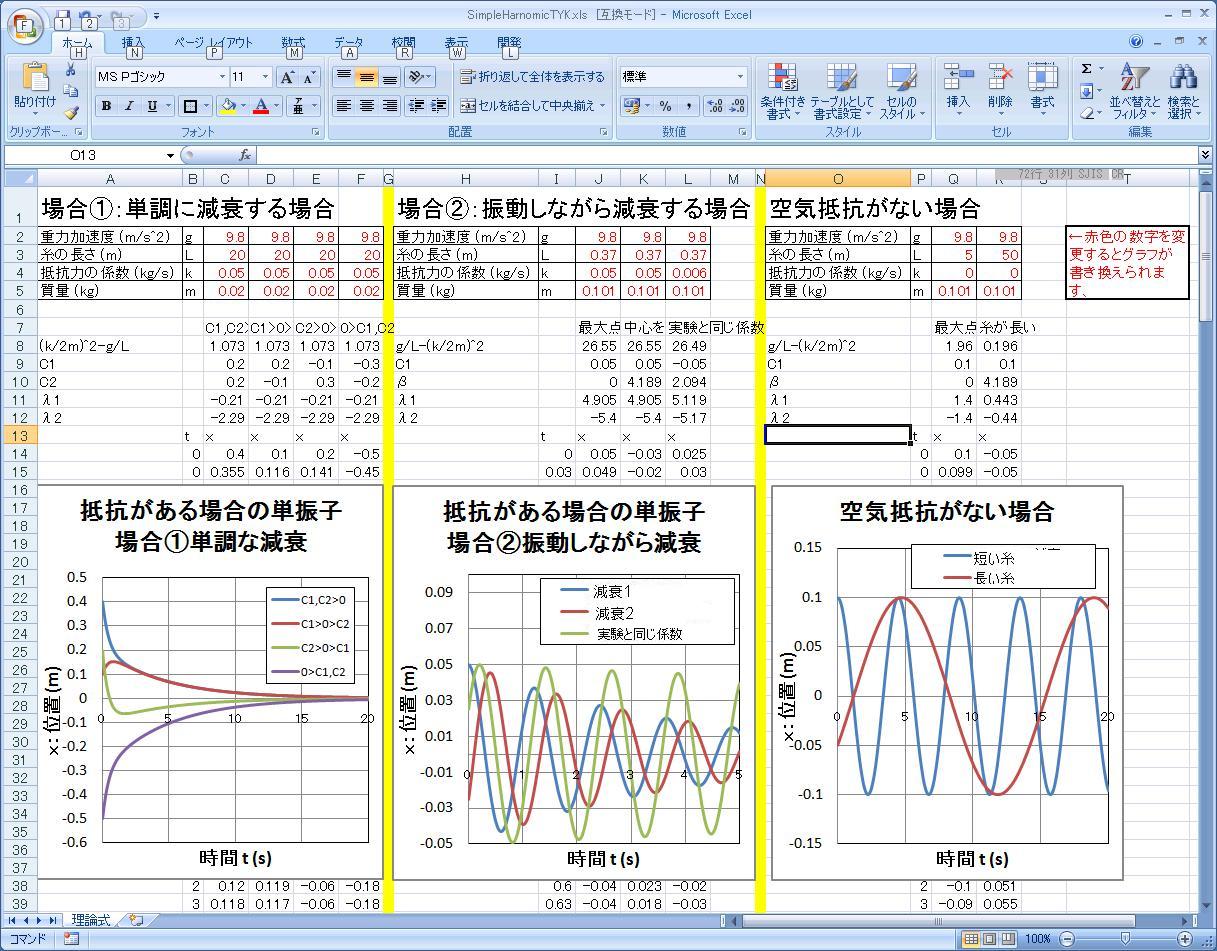
この減衰のない単振動を グラフにしたのが以下の図になります。 計算に用いた係数を記入してあります。
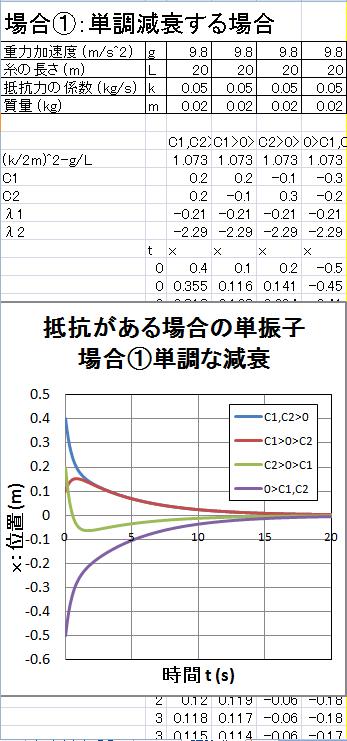
減衰がある場合には扱いはかなり複雑になります。 今回は速度に比例した減衰力を受ける場合を解きます。

では、これらを2通りの条件に分けて考えてみましょう。

ここで得られた、一度限りで振り子が運動を停止(無限に速度が小さくなる)し、 振動を伴わない解は以下の図で表されます。
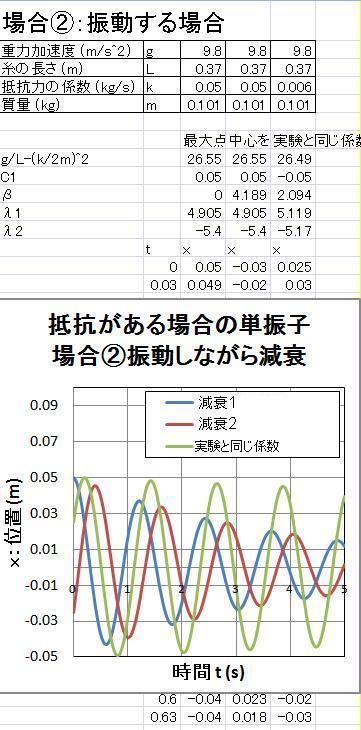
いわゆる、普通の振り子の方程式です。 振動しながら減衰していく解は以下のように得られます。

ここで得られた、減衰を伴う振動は解は以下の図で表されます。
を作成いたしました。高校の科学クラブなどでご活用ください。 急いで解いたのでミスがあるかもしれません。 ご指摘いただければ修正させていただきます。
ここで公開するアイデア/装置は安全性を保障しておりません。 用途に応じた設計を行い、十分な安全検査を行ってからご利用ください。 本サイトの情報の営利目的での利用はご遠慮ください。 本サイトの内容の無断転載を禁じます。© 2011 TYK