
エクセルのマクロ機能を用いて 文章を簡単に暗号化するソフトを作成いたしました。日本語にも対応しております。やや文字列は長くなりますが、毎回異なる暗号が作成されます。暗号はコピーのしやすさを考慮して英数字記号のみを用いて表現しました。特別な秘匿性を求められる用途には、乱数列を変更したものを作成いたしますのでご連絡ください。
こちらからダウンロード可能です↓
暗号化エクセルマクロTYKCodeMaker2.xls
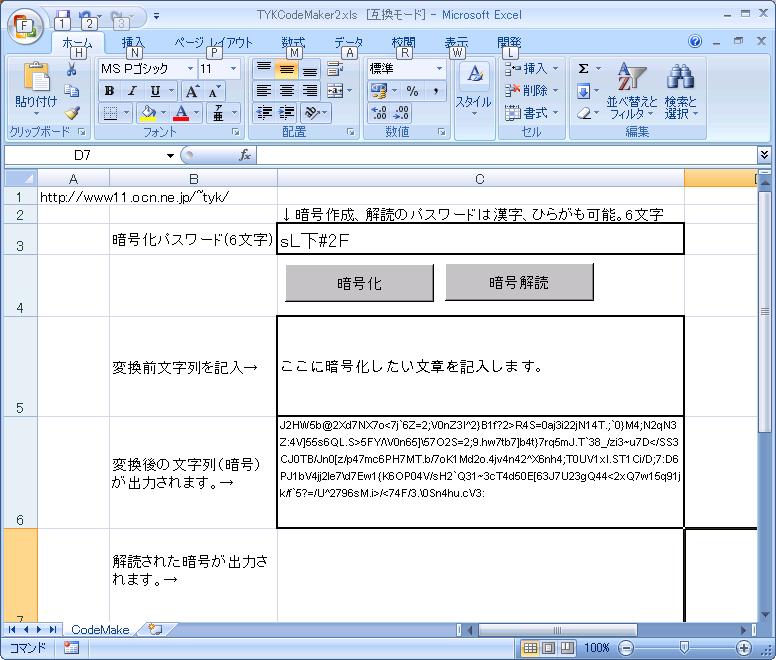
最近、旧ドイツ軍で使われていた エニグマ・コードに関する本を読み、簡単な暗号を作成してみようと 思い立ちました。実際にプログラムを書いてみますと、 複雑な式を用いて暗号を作成(Coding)するのは比較的容易でした。 しかしながら、暗号を解読する(Decoding)は式が複雑であれば あるほど、(アルゴリズムは理解していたとしても)大変な作業となりました。 本サイトで配布するソフトのパスワードとしても使われている ワンタイムパスワードの使用では、与えられた情報から できる限り複雑で誰も思いつかないような式を組み合わせて、 復号できないようなアルゴリズムを作ります。 暗号化前のパスワードが読めなくて良いのか?と疑問になるところですが、 このような使用では問題になりません。 ソフトをインストールする時に使用するパスワードのように配布し(このサイトの例では月ごとのパスワード)、 それを暗号のまま記入し、 ソフトウェア内で元の情報(ここでは時間情報)から暗号を作成し、 暗号同士を比較するという方法をとります。 こうすることで暗号化するプログラム自身を秘匿すれば、 他者に次の(他の)パスワードを作成されることを防ぐことができます。
今回は6文字のパスワードを用いて 一定の文字列を暗号化し、 暗号を受信した人がパスワードを知っている場合にのみ 暗号が解読できるというシステムを作成いたしました。 特定の文字を別の文字に一対一に交換するという換字式の アルゴリズムを用いましたので、エクセルシートの2枚目に換字表を 付け加えました。ですから、実際には換字表を変換してしまえば 暗号は全く読めなくなってしまいます。 ですから、正確には「パスワード」+「換字表」を送受信者で 共有していることが暗号解読の条件になります。 練習用として作成した最初のエクセルファイル(TYKCodeMaker.xls)を以下からダウンロードして取り出してください。 本プログラムでは簡単な暗号化1つ(文字列を逆転させる:Abc→cbA)と 換字表をそれぞれの文字に複数回施す処理を行っています。 やや複雑なものですがアルゴリズムも公開していますので 重要な情報の秘匿には使用しないほうが安全かと思います。
文字を逆にするだけでも、一瞬では元の文章と判断するのは難しくなります。 非常に単純な操作ですが、これを最初に入れておけば、 換字式の暗号で第三者が解読しようとするときに 文字列が意味をなすものか否かが判断しにくくなります。
本プログラムでは以下のように記述しました。
文字列をsentenceで与え、その長さをLengthSentence=Len(sentence)で
与えた時に
For i = 1 To LengthSentence
CodeDiv = Mid(sentence, i, 1)
Code = CodeDiv & Code
Next i
なる操作を与えています。
今回は元の文字列を
「Nice to meet you!」
で与えます。これを変換したものは
「!uoy teem ot eciN」
となります。
鏡に写した文字のように見えますが、
文字自体は当然、普通のアルファベットで
並び方が逆になっただけです。
エクセルの"換字表"シートのような表を用意します。 今回は文字列それぞれに0から1までの乱数を与え、 乱数の小さい順に並び変えるという方法で 文字が一対一に変換される表を作成しました。 作成する方法は他にもありますが、 同じ文字が2度使われると解読が不可能になりますので注意が必要です。 逆にいえば、上述の、解読する必要がない暗号(パスワードのようなもの)を作成するには 意図してこういったテクニックを使用することも良いと思われます。 今回は95文字を使用しましたので、表は95!=95*94*93*92*...3*2*1通りの組み合わせが あることが分かります(*は掛け算記号です。)。これは計算しにくいですが、
スターリングの近似式ln(n!)=n*ln(n)-n
を用いると95!≒exp(337)≒10^(146.6)程度となります。146桁の組み合わせがありますので この換字表をコンピューターでしらみつぶしに解くことはほとんど不可能となります。 146桁という数字は想像しにくいですが、1兆(1,000,000,000,000)が13桁の 数字ですから、一兆を11回ほど掛け合わせた数字となります。
元の文字列
「!uoy teem ot eciN」
は
「yM3R_" '_3"_ Oin」
となります。
複数回出てくる
eが空欄(スペース)に
変換されていることがわかります。
tは"に変換されています。
146桁だから大丈夫、とは言えません。英文の中に頻出するスペースやa theなどの
文字の組み合わせから、換字表を少しずつ推測することが可能であるからです。
そのためにもう一つの工夫をいたしました。
それは、文字の変換を複数回行う手法です。
実際には暗号化と解読のパスワードから
得られる20程度の数字の回数だけ換字を行うことで、元の換字表を
推測しにくくします。しかしながら、一対一の変換では元の換字表を
知らなくても、複数回の変換の最初と最後さえ推測できれば
文字を元に戻すことが可能であるとわかります。
そこで、この回数を、一文字ずつ変化させていく手法をとります。
具体的には暗号化と解読のパスワードから、変換のパラメーター(no1)を取り出し、
ConvFactor = (i * no1 + 1) Mod 13
i番目の文字に対してCOnvFactorの回数だけ変換を行います。
こうすることで、変換はより複雑になり、暗号解読が困難となります。
例えばno1=9の時には、i=2番目の文字に対して
9*2+1=19割る13で余り6となり、6回の変換を、
i=3番目の文字に対しては
9*3+1=28割る13で2となり、2回の変換を行います。
ここで13を用いたことに大きな意味はありません。
文字列が大きくなったときに多数回の変換を行うのが計算時間が
たくさんかかってしまうことを防ぐためです。
mod 13とすることで0から12までの数値をとりますので、
一枚の換字表を0回から12回使用した状態で暗号を作成していることになり、
安全性はずっと高くなります。
具体的なコードは
LengthSentence = Len(sentence)
For i = 1 To LengthSentence
CodeDiv = Mid(sentence, i, 1)
ConvFactor = (i * no1 + 1) Mod 13
For j = 1 To ConvFactor
CodeDiv = CodingTYK(CodeDiv)
Next j
Code2 = Code2 & CodeDiv
Next i
CodingSentenceTYK2 = Code2
としました。関数CodingTYK(CodeDiv) は与えられた一文字(CodeDiv)を 換字表に基づいて一回だけ変換する操作を行います。
元の文字列
「yM3R_" '_3"_ Oin」
は
「!TIsB',Es#wX|e=iS」
となります。
文字が一対一に対応しなくなりますので
no1やConvFactorの算出法を公開しなければ
解読するのは困難となります。
最終的にはさらにこのような一文字ごとの変換を
他の回数だけ繰り返す処理を加えて冒頭の
S5)~n?{rmd9U|$Mik
を作成しました。文字数だけは分かる、という状況ですが、
変換に用いたno1のような数値の導出方法なしでこれを解読するのは
ほぼ不可能だと思います。単一の文字に対して暗号化パスワードを
少しずつ変化させながら暗号化された文字がどのように変化するかを
見ていけば少しはアルゴリズムが推測がつくかもしれませんが、
パスワード無しで解読するのは非常に困難であると思われます。
エクセルシートでは「解読」機能も付与しました。 上述の操作を逆の順序で行うことで元の文字列に復号することができます。 暗号文字列を少しずつ変えて復号する操作を繰り返すことで、 アルゴリズムに推測がつきやすくなり、危険度は高くなります。
最後に、実際に解読が困難であることを示すために以下の
暗号を示します。アルゴリズムは公開されたソフトと同一です。
換字表は変更してあります。
解読できた方がいらっしゃっいましたらメールにて元の文字列をご連絡ください。
文字数は44文字です。
薄謝進呈いたします。(`)と(d)の間はスペースが二つ続いています。
現在、文字数も変更され、
日本語を含む全ての文字コードに対応した
より安全なソフトを作成していますので
それまでに破られなければ良いのですが。
ここで公開するアイデア/装置は安全性を保障しておりません。 用途に応じた設計を行い、十分な安全検査を行ってからご利用ください。 本サイトの情報の営利目的での利用はご遠慮ください。 本サイトの内容の無断転載を禁じます。© 2009 TYK