 目次へ
目次へ
2011年1月15日の朝日新聞夕刊のbe eveningで 「2×8ならタコ2本足」と題する特集記事を 読みました。 掲載されたのは「花まる先生(公開授業)」が児童の興味を高める方法を工夫して授業を行っている取り組みを紹介するコーナーです。 私も楽しみに読んでおります。 今回の記事や方法について、良くないと感じる部分がありましたので、 計算の方法、算数の教え方について考察(主張)してみたいと思います。
本記事において、典型的な計算の誤りとして以下の例が挙げられています。 「飴を3個買います、1個5円の飴を買うと全部でいくら(何円)?」という問いかけに対して 「3×5」と答えることは、かけ算の意味を理解してない誤りとされています。 登場する「花まる」先生の狙いは、 「何のいくつ分」という考え方を理解させることであり、 この問いに対する答えとして「3×5」(3個×5円)は誤りであり、「5×3」(5円×3個)が 正しい答えであると教えているとのことでした。記事では てんとう虫の足の数やウサギの耳の数などの 同様の例が繰り返し出されます。 「2×8ならタコの2本足」というタイトルは、これらの例のように、 かけ算の順序を考えることが重要であるとの主張を端的に示しています。 別枠の「はってん はっけん」では「映像を思い浮かべて計算」することが 思考力を高めるために有効であるとの主張がなされています。
こうした算数の教え方の良いところが「思考力を高める」点にあるという主張には納得できます。 何も考えずに、出てきた数字だけを見て九九を思い出すだけよりは、タコの姿などの実際の物を想像する方が、 思考力を要することに間違いはないでしょう。しかし、残念なことに、数字を扱うということは 物から離れた抽象的な思考をする訓練であるという側面が完全に忘れ去られています。 タコの足であろうと、てんとう虫の足であろうと、 人口であろうと、気温であろうと、数値に置き換えられるものは全て同列に扱うことが 出来ます。こうした抽象的な思考を行う能力こそが、 社会で生きていくために絶対に必要であり、 より高度に数字を扱う職業(今の日本で、物から離れた数字を全く扱わない仕事はあまりないのではないでしょうか)において 求められる算数の能力に他ならないからです。算数を勉強する過程で、 少しずつ、少しずつ具象を離れて、抽象に近づかなくてはなりません。 そのためには、九九を覚えた時点で、かけ算の結果は、 (論理的にも単なる数字の上でも)その順序によらないことを、 理解しなければならないのです。 かけ算は、タコの足の数を数えるような 具体的な方法から抜け出し、 二つの数字を使う単なる演算の一つとして理解しなければならないのです。
「かけ算の答えは論理的にも単なる数字の上でも、その順序によらない」ことを説明したいと思います。 「2匹のタコがいます。タコの足は8本です。全部で何本の足があるでしょう。」 この問いに対して「8×2」は正解です。「8本足のタコが2匹いる」からです。 しかし、「花まる先生」に「計算を理解していない」と叱られてしまう 「2×8」も同様に正解です。なぜでしょうか?このように考えることが出来るからです。 それぞれのタコの足に「ア」、「イ」、「ウ」、「エ」、「オ」、「カ」、「キ」、「ク」とマジックで印をつけます。「ア」の足は2本あります。同様に「イ」も2本あります。 「2本の足が8種類ある。」だから「2×8」でも同じ答えになるのです。 ですから、かけ算というものが、「同じ数の足し算を複数回行う」演算であることを理解していれば、 順序によらないことは、いつでも(難しい言葉を使えば普遍的に)成立し、 否定する理由は全くないことがわかります。 全てのかけ算でこのような論理の変換が可能だからこそ、かけ算の順序は変えても良いのです。。
かけ算が行っている作業を再確認させるためにタコの足を持ち出すこと自体は悪くはありませんが、 かけ算を演算という抽象にまできちんと昇華させる説明を飛ばして、 「2×8」を否定するのは教育の方法として良くないと考えます。 繰り返しになりますが、少しずつ少しずつ抽象化して、 数を単なる数としてとらえていくことが 算数で身につけるべき能力だと考えらます。 これは、「モノ」から「コト」への 変換と言いかえることができますでしょうか。 ですから、この計算がかけ算により演算可能である(順序によらない)ことを理解している時点で どのような順番で計算しても正解なのです。
いきなりの抽象化は難しいです。当然、 小学2年生では具象、具象、で進めればで大丈夫です。 最初は指を折って数えるしか方法がないかもしれません。 しかし、これからより複雑な算数や数学に発展していくためには、具象は大きな妨げになります。 表にしたり、図形が出たり、グラフに描いたりするようになった時点で、全く 答えが分からなくなる児童が多いのは、今回のような具象への過度の信仰(まさに「信仰」としか言いようがありませんね。)があるからだと思われます。 残念ながら、世の中のほとんどの数はダイレクトに思い浮かべることが出来ず、 そのために抽象化が必要となるのです。
驚く児童、新しいことを教えた(ような気分になる)先生、 それはほほえましい場面で、児童の興味も高まるでしょう。 しかし、そのテクニックに酔って、子供たちが自然に抽象へと 羽ばたく可能性を奪ってはいないでしょうか。 その教え方は、子供たちのためではなく、 教える側の満足のために選択しているものではないでしょうか。
数字にした時点で、すでに具体的なものから離れているのです。 わざわざ引き戻すことはないのです。 抽象化しなければ、極めて非効率で、なおかつ発展性が無くなってしまうのです。 繰り返し練習することで数の具体的な姿を無視できるようになり、 そこで初めて新しいステップでの想像力が働くようになるのではないでしょうか。 変な例ですが、 アメリカ人(全てのアメリカ人に当てはまるのではなく、差別的な表現ですが)の 店員さんが、お釣りの計算に「ある変なやり方」をするのを目にしたことはありませんか? 彼らは「お札を数えながら、代金に足していき、合計が相手が出した額と同じになる」という 方法で引き算を計算をします。引き算が足し算の逆演算であることを巧みに利用して、 抽象化を逃れているのです。
例)85ドルの物を買って、100ドル札で払ったときに、 店員さんがまず10ドル札を出して、「95(85+10)」と読みあげ、そこから1ドル札を 1枚ずつ声に出しながら「96」、「97」、「98」、「99」、「100」と数えて15ドルの おつりを準備することがあります。これは、100-15を暗算できないことに起因していますが、 数字と物を一対一に対応させることでしか計算ができないという、 「具象から抜け出ていない」状態を端的に表しています。もちろん、この程度であれば何の問題もありません。 計算をする度に絵を描いたり、物を数えたり、指を折ったりすれば良いだけです。 しかし、日常生活はもちろん、仕事として具体化出来ない数字は数限りなくあります。 いえ、現代の普通の生活を送ろうとすれば、数字の大半は具体化できないのです。 だからこそ、これから教育を受ける子供には、この例のような大人になってほしくないのです。
例えば次の問いを考えてみます。
「地球上の人口は現在6900000000人です。100年後には2倍になると予想されています。何人でしょう。」
黒板に6900000000の人のマークを描くことはできません。いくらなんでも多すぎます。
しかし、1億人の大きな人を69人分
描くことはできます。ですから、69×2(億人)=138(億人)、と計算出来ます。
100000000=1億の変換にこそ、想像力を使うべきではないでしょうか。
6900000000の映像を思い浮かべることは不可能であるからこそ、抽象化の重要性が理解出来るのです。
こういう計算も出来ます、69億人と書いた、一つの人のマークを描きます。
これをもう一つ描きます(2倍になる)。これも69×2です。実物を思い描く必要はないですし、
数字を単なる数字のみとして扱っています。当然、2×6900000000も正解であることを示せます。
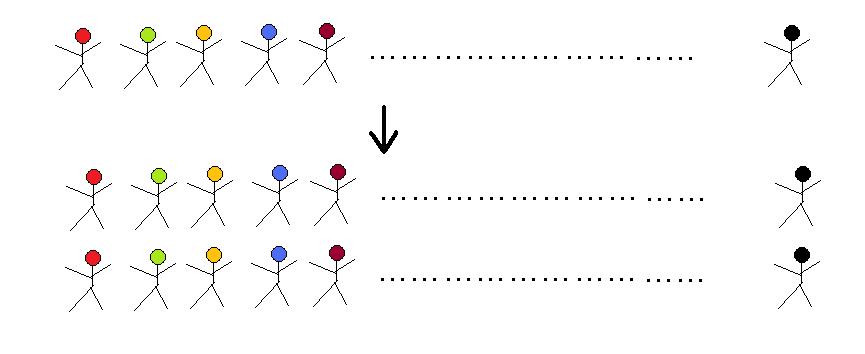
人のマークを5つほど黒板に描きます。後は点々でたくさん人がいることを推測させます(下図)。
これが2倍という演算により、矢印の下になります。2人一組の人が6900000000組いるから
2×6900000000も正解であると簡潔に説明できます。小学校3年生には計算できないですか?
2×6900000000=2×(69億)=(2×69)億=(69+69)億=138億です。
3年生にも出来ますね。下のように考えると、応用範囲は広がります。
ほとんど同じように見えますが、論理の抽象度は格段に高くなりますね。
(×1億)の考え方、できるでしょうか。
2×6900000000=2×(69億)=2×(69×1億)=(2×69)×1億=(69+69)×1億=138×1億=138億
69+69が計算できませんか?
69+69=60+9+60+9=60+60+9+9=(60+60)+(9+9)=138。
小学校3年生にもできますね。足し算も順序には依存しませんね。
60+60が計算できませんか?
60+60=6*10が2つ=6*10*2=6*2*10=12*10=120
競争心に依存する
「100マス計算」なんかを持ち出さなくても、計算の練習はいくらでも出来ます。
競争は負ける子供にとってはは辛いことですし、それでますます苦手になりますよね。
そもそも、今の日本の社会では、計算の速さのような機械的な能力の重要性は下がり、
人それぞれで異なる個性や物のとらえ方(感性)の方が重要となってきているような気がします。
この時代に競争を促して一面的な能力を向上させたり、
掛け算の順序のような画一化をすることが子供たちにプラスになるでしょうか。
かけ算の方法論は別にして、
この記事を読んだ時の私自身の違和感や反感の理由を考えてみますと、
教育の捉え方の相違にあることに気付きました。
当たり前のことですが、子供は常識にとらわれません。
「正しい」やり方や一般的な方法を「まだ」経験し体得していないからです。
この、正しく一般的な方法を子供に「叩き込む」のは教育の重要な側面です。
そうでなければ、社会で生きていけない大人になってしまいます。
社会のルールや方法に従うことは後天的な能力であり、(家庭、学校、地域社会などの)
教育のみでしか身に付かないからです。(動物と人間の違いを思い浮かべてください。)
しかし、根本的な誤りでなければ、子供のやり方を
ことさらに否定したり、常識的な方法が唯一の解であるなどと強調する必要はないと思うのです。
一般的なやり方は極めて強力です。人類が引き継いできた素晴らしいものです。
しかし、文化や経済、学術等の発展は、一般的でなくオリジナルな発想や方法と、
それを許容してきた人間の寛容の上にのみ成り立っているように思うのです。
教育の場でこそ、児童の発想に「不正解」の烙印を押すことは慎重に吟味されてしかるべきです。
ましてや、今回のかけ算は絶対的に正しい方法なのですから、否定される理由は皆無です。
今回の記事のような教え方はその点で、ずるいし弊害が大きいと思うのです。
(談)に「ウサギの耳の数、人の鼻や指の数など、間違えると明らかにおかしいものを選びます。
インパクトが強ければ、今後もかけ算を考えるときに、映像が頭に残りますから」
と書かれているように、作戦は周到で(これ自体は悪いことではありませんが)、
狡猾な方法であり、子供に対して行う教育としては不適切だと思うのです。
発想を自由にすれば、どのようにでも考えられるかけ算において、
一見すると論理が誤っているように見える特異な例を予め選んでおいて、
「君の答え、考え方は間違いです」という風にやるわけです。
圧倒的に立場の弱い児童に対して、
先生が論理が成立したように見える特異な例だけを強く示すことで、
自由な発想の子供が持つ、無限の可能性を否定しているように感じるのです。
再度繰り返しますが、どのようなかけ算も順序を変えて論理的に説明できますし、
「今後もかけ算を考えるときに、映像が頭に残」ることは、
その子供の、数を扱う能力の今後の発展に
負の影響を与えかねません。もし、具体的に物を思い浮かべることが重要で、
計算を特定の意味(具象)に結びつける重要性を主張するのならば、例えば
5年生での”分数での割り算”はどう教えるのでしょうか?
その瞬間に、すべての具象を忘れて、(この例は仕方のないものだから)
何も考えずに暗記しなさいと教えるのでしょうか?
(私、論理を通して具象に結びつける方法を明確に答えられますが、かなり難しいですよね。)。
5÷(2/3)や(2/3)÷(1/15)は、これまでの算数ではない、
別の世界のものとして教えなければならないのでしょうか。
そんな、いつもその場限りの大人の論理を敏感に感じ、
子供は興味を失ってしまうのではないでしょうか。
ここで公開するアイデア/装置は安全性を保障しておりません。 用途に応じた設計を行い、十分な安全検査を行ってからご利用ください。 本サイトの情報の営利目的での利用はご遠慮ください。 本サイトの内容の無断転載を禁じます。© 2011 TYK