目次へ
目次へ
毎朝ご飯を炊くのは大変ですね。 一般的な方法かと思われますが、週末などに多めに炊いておいて、 一食分ずつラップでパックして冷凍しています。 これを電子レンジで2分間解凍すれば、準炊きたてのご飯(quasi-as-cooked rice)が出来上がります。 農家の方にお聞きしても「冷凍ご飯は味があまり落ちない」との ことですので、それほど悪くない方法かと思われます。 今回は保存に便利なきれいな包み方を示し、 様々な計測値における平均と標準偏差の求め方を考察するため、 ごはんパックの質量の分布を求めました。2011, Aug 31.
準備するものはサランラップのみです。材質により、包みにくいものもありますが、 それほど問題にはなりません。ご飯は炊きたてをすぐに包んで、 あら熱を取ったら急冷するのがベストのようです。
1、ラップを調理台やまな板の上に広げます。 20-25 cm幅のラップで正方形よりやや長いくらいがちょうどよいです。

2、ご飯をラップの中央に載せます。 ここでは小さい茶碗に一杯分です。

3、厚さ2 cm程度の正方形に整えます。 薄くするのは、冷却を早めるためです。 また、定まった形とすることで、冷凍庫での保存において無駄なスペースが生じません。 あまり押しつぶすとよくありません。

4、下を折り返します。この時に、ラップの上から 手のひらで正方形の一辺を整えます。

5、同様にして、上の辺、右の辺、左の辺を折り返して包みます。


6、わずが数秒でご飯ラップの完成です。

下図のように、金属製の調理台など、 伝熱の良いところに置いて、あら熱を取ります。 温かさが無くなったら冷凍庫に入れます。(厚いまま入れてしまいますと、 庫内の温度が上昇するだけでなく、非常に大きな電力を消費します。) 急冷するためのこつは、広い冷凍庫に分散して配置することです。 保冷剤などで挟んでもよいかもしれませんね。

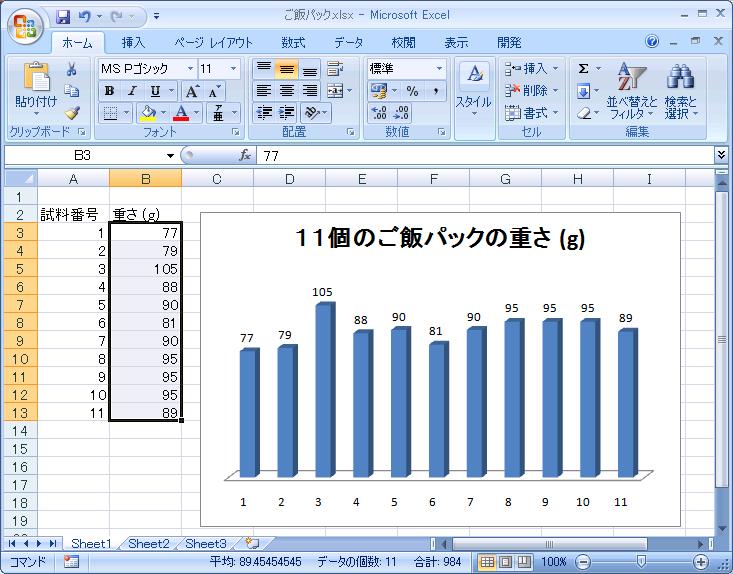
3合のご飯を炊いて、目分量で11個のご飯パックを 作りました。これがどの程度均一に包まれているかを 調理用はかりにて検証いたしました。 得られた11個のデータは以下の通りです。
77, 79, 105, 88, 90, 81, 90, 95, 95, 94, 89 (g)

データをエクセルに記入します。試料番号は特に必要ありません。
単純な棒グラフを作ってみましょう。 左クリックを押したまま複数のデータを選択できます。 これで、重さのデータを選択します。 そして、上のバーから「挿入」-「グラフ」-「縦棒」を選ぶことで グラフが描かれます。
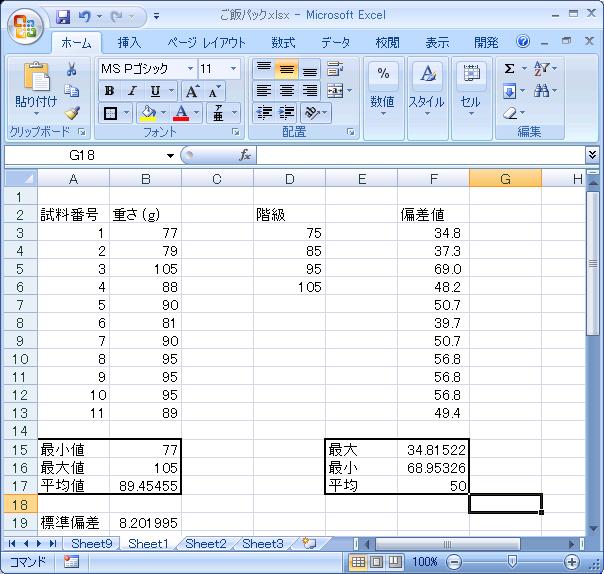
分析の基本として、最小値と最大値、平均値を求めてみましょう。 最小値を記入したいセルで=MIN()と記入し、かっこの中をクリックしてデータを選択します。 ここではB列の3行から13行にデータがありますので=MIN(B3:B13)となります。 同様に、最大では=MAX(B3:B13)、平均値は=AVERAGE(B3:B13)とします。 今回のような少ないデータでは最小、最大もすぐに見つけ出せますが、 自動に取得した100個以上のデータでは人が見つけるのは大変ですね。 PCに任せれば一瞬です。平均は89.45 gと求まりました。
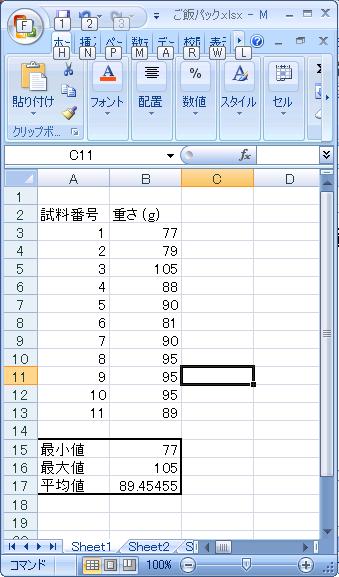
つぎに、ヒストグラム(度数分布図、どの程度の値がたくさんあるかを示す)を分析してみましょう。 ヒストグラムを作製するにはややデータが少ないですが、 分析は可能です。 先ほど、データの範囲が77-105に収まることがわかりましたので、 例として、75, 85, 95, 105を階級といたします。すなわち、全てのデータが75-85, 85-95, 95-105, 105以上のどの 範囲(階級)に属するかを分析します。 下の図のように、「階級」というデータを自分で作ります。最小値から 初めます。「データ」-「データ分析」-「ヒストグラム」を選びます。
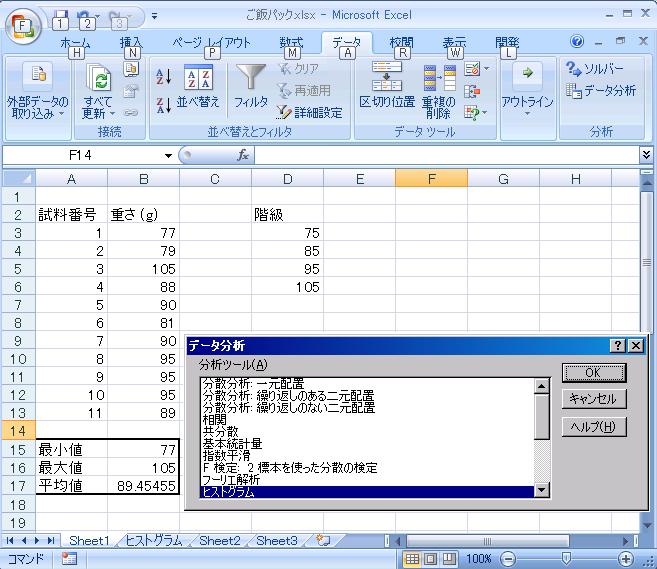
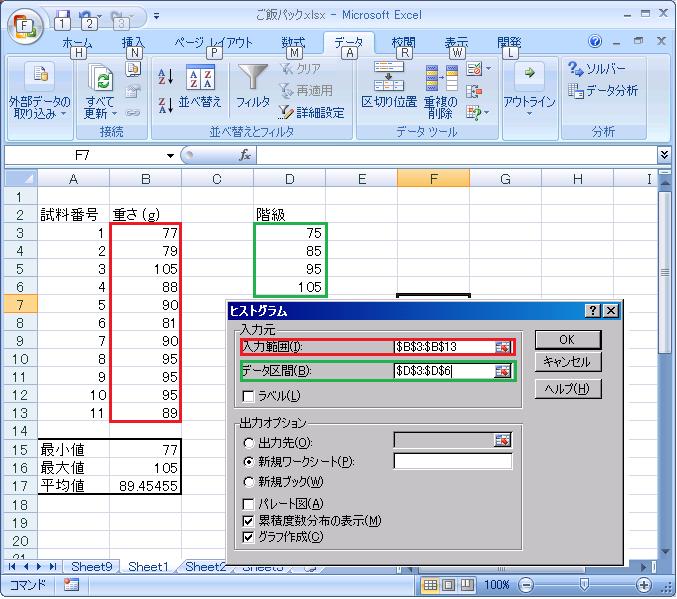
ここで、「入力範囲」として、データの数列を選択します。 さらに、「データ区間」として先ほど作製しました階級のデータを選択します。
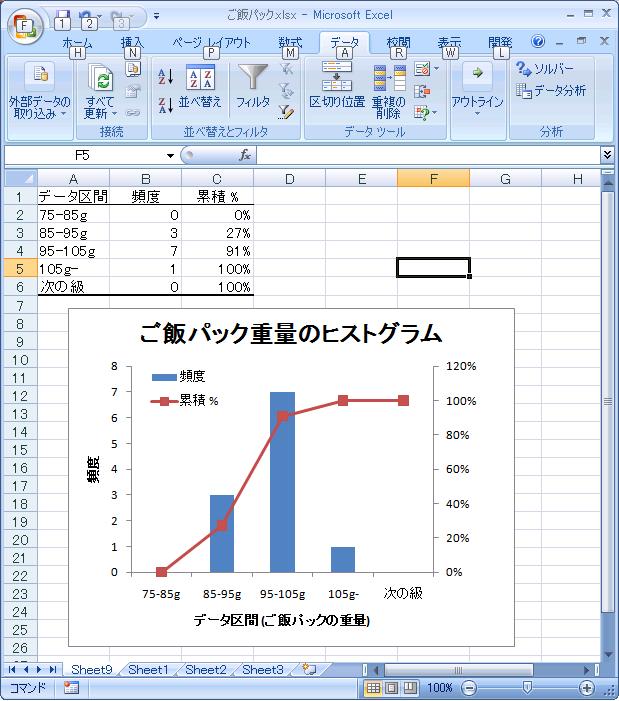
これにより、自動でご飯パック重量のヒストグラムが作製されます。 横軸にデータの範囲、縦軸に頻度(そのデータの数)の棒グラフが作製されています。 さらに、累積頻度も折れ線グラフとして表示され、例えば105 g以下のデータが全体の 91%を占めることも分かります。
データの意味は難しいですが、標準偏差もEXCELの関数として準備されています。 =STDEV(B3:B13) (standard deviation)とすることで、8.2という 答えが返ってきます。これをもとに各データに対して偏差値を求めてみましょう。 偏差値は平均が50で標準偏差分離れると10上がるという数値 (100以上も負もありうる)で
50+10*(データ - 平均)/標準偏差
で求められますね。データを見ますと、最軽量の77 gは偏差値34.8です。 最も高い偏差値は105 gに対する69.0であるとわかります。 もちろん、偏差値の平均は50となります。
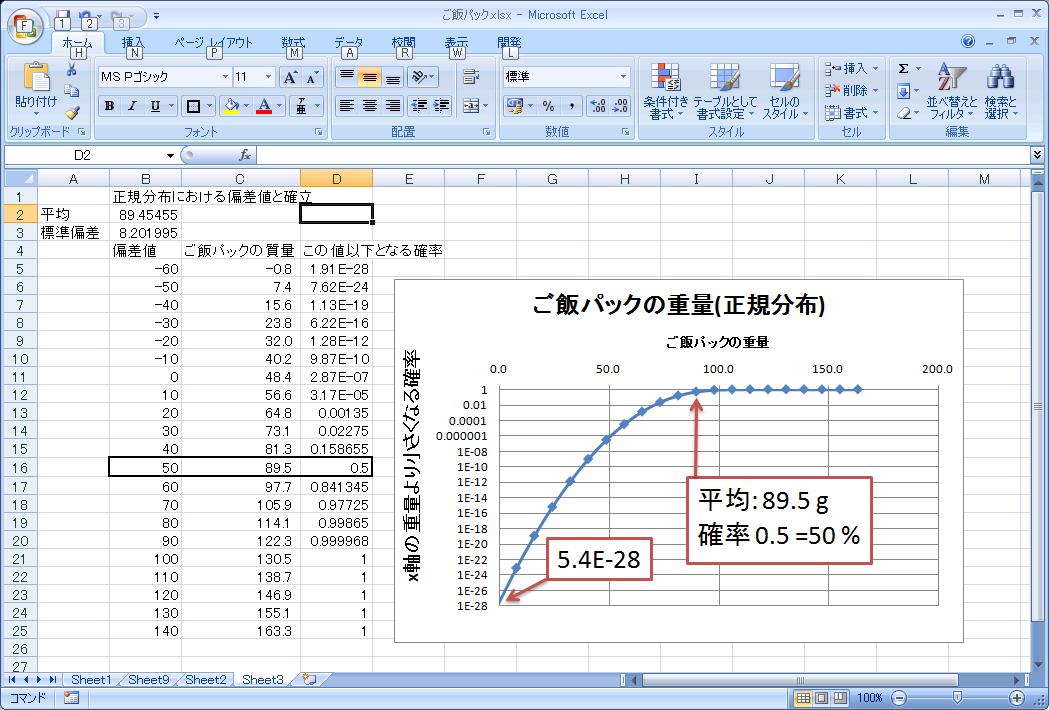
このように、11個のご飯パックの重量から 得られるデータとしては89.5 ±8.2 gを得ました。 8.2 gは標準偏差である。 (今回のデータに限らず)ご飯パックの重量が正規分布をしていると仮定すると 89.5 ±8.2 gに68.3%、 89.5 ±16.4 gに95.4%のご飯パックが入ることが分かります。 前者が偏差値40-60、後者が偏差値30-70の範囲に入ります。
ご飯パックの質量にばらつきがある限り、 一粒のご飯粒も入っていない空ご飯パック(Vacant rice pack)が製造される 可能性もあります。正規分布を仮定すれば、この確率も容易に算出できます。
平均値/標準偏差=89.5/8.2=10.90が求まります。 これは、標準偏差の10.9倍のいちにある値において、ご飯パックの質量が0または2倍になることを意味します。 偏差値でいえば、-50.9(重量0)もしくは159(重量2倍)となります。 標準正規分布の累積分布関数は=NORMSDIST(値)で求めることが出来ます。ここでの [値]は平均が0、標準偏差が1に規格化されていますので、 例えば
NORMSDIST(0)=0.5 (平均以上は半分)
NORMSDIST(1)=0.841 (偏差値で60以下は84.1 %)
NORMSDIST(2)=0.977 (偏差値で70以下は97.7 %)
のような値となります。今回は重量0のご飯パック、 すなわち、平均から標準の10.9倍分、 低いところに外れる可能性として、 NORMSDIST(-10.9)=5.4E-28の解が得られます。 逆数にすると、1.9E27=1,900,000,000,000,000,000,000,000,000 となります。すなわち、10億個のご飯パックのセットを10億個作り、 さらにそれを19億個作った時、その中に1個だけ空のご飯パックが製造されうる ことを意味しています。もちろん、正規分布が当てはまることを 証明するには、たくさんのご飯パックを作る必要もありますし、 分布のスソが正規分布に乗る必然性もありません。