
2次元実平面上の任意の座標(x,y)に点を作ります。 この時、最寄りの格子点((0,0)や(3,-5)などの 整数の点)までの距離は平均的にはどの程度になるかを考えました。 解法は複数あるかと思いますが、今回は①解析的な積分と②数値計算の 二通りの方法で解きました。答えはπや分数では表せませんでした。 ご自身で計算されたい方は以下の解答は見ないで考え始めてください。
Updated on June 26, 2010
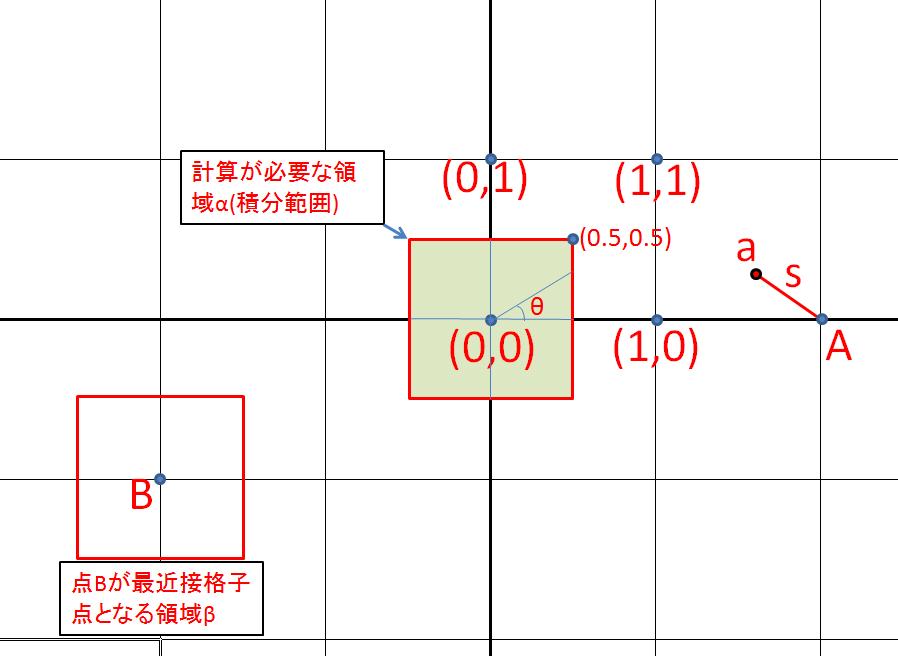
問題を整理すると簡単になります。下の図には
座標原点近傍の格子点やランダムに作製した点を描いています。
例えば、座標上にa点が選ばれた時には、最近接の格子点はAとなりますので
そこまでの距離はsとなります。逆に考えると、
格子点Bが最近接となる領域は左の赤の領域βとなります。
このように考えますと、
座標上の全ての点は(-0.5,-0.5),(0.5,0.5),(0.5,-0.5),(-0.5,0.5)の
領域内に落ちたと考えて、そこから近接点までの
距離を考えるだけで良いことが分かります。
すなわち、最近接点が原点となるのは
緑色の領域αです。すなわち、
L=(x^2+y^2)^0.5
をこの領域の中で積分すれば良いことがわかります。(^0.5は√です。)
「答えはπ」とか「1/2」と思ってはいけません。
積分領域が円ではなく、四角ですから
暗算では難しいと思います。
ここからは数式が多くなります。 secθ=1/cosθなどが出てきますが、 高校数学の発展か、大学1年程度で習うのではないでしょうか。 下記のように解きました。






これまでの式に間違いはないように思いますが、 これを数値積分と乱数を用いた数値シミュレーションの 2通りで解き、答えが正しいかを検証します。
乱数を発生させるのは簡単ですから、 モンテ・カルロ法で解いてみましょう。 例えば、(0,0),(1,0),(1,1)(0,1)を頂点とする 正方形のみを考えて、この中に点が形成された時の 格子点までの平均距離を求めます。 乱数シミュレーションソフトウェア からエクセルで実行できるシミュレーションソフトがダウンロードできます。 マクロを有効にしてご使用ください。1シート目には 乱数を生成して最寄りの格子点を求め、そこまでの距離の平均値を出すプログラムが記載されています。 プログラムの速度を上げるためにグラフ化機能を無くして、 最寄りの格子点までの距離の平均値のみを表示したものがシート2にあります。 シート3には、∫ sec^3 θ dθの簡易的な数値計算の結果を示してあります。 いずれの場合にも上の解析的な解と同じ値となっております。
プログラムを動作させた例↓ダウンロードして遊んでみてください。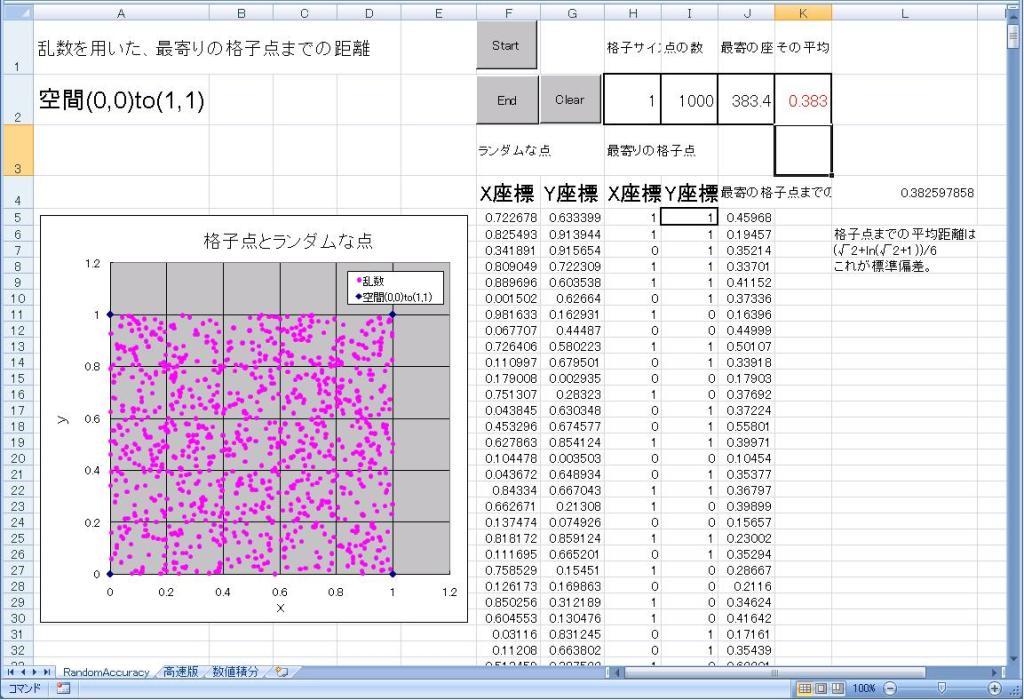
ここで公開するアイデア/装置は安全性を保障しておりません。 用途に応じた設計を行い、十分な安全検査を行ってからご利用ください。 本サイトの情報の営利目的での利用はご遠慮ください。 本サイトの内容の無断転載を禁じます。© 2010 TYK